Inspirasi Terbaru Luas Segitiga Sama Sisi
Januari 08, 2022
Inspirasi Terbaru Luas Segitiga Sama Sisi

Rumus luas segitiga dan keliling segitiga Fisika dan Sumber : fismath.com
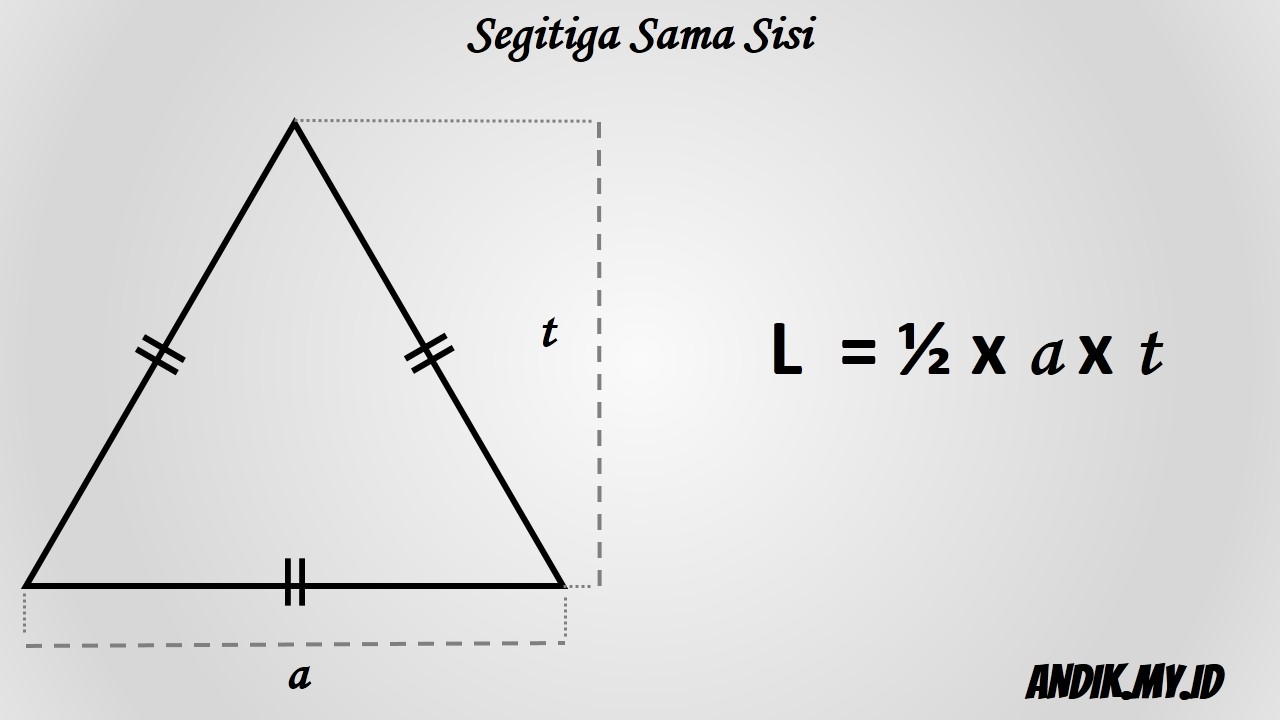
Cara Menghitung Luas Segitiga dan Keliling Segitiga Sumber : www.andik.my.id

Rumus Luas dan Keliling Segitiga Sama Sisi Trimatematika Sumber : trimatematika.wordpress.com
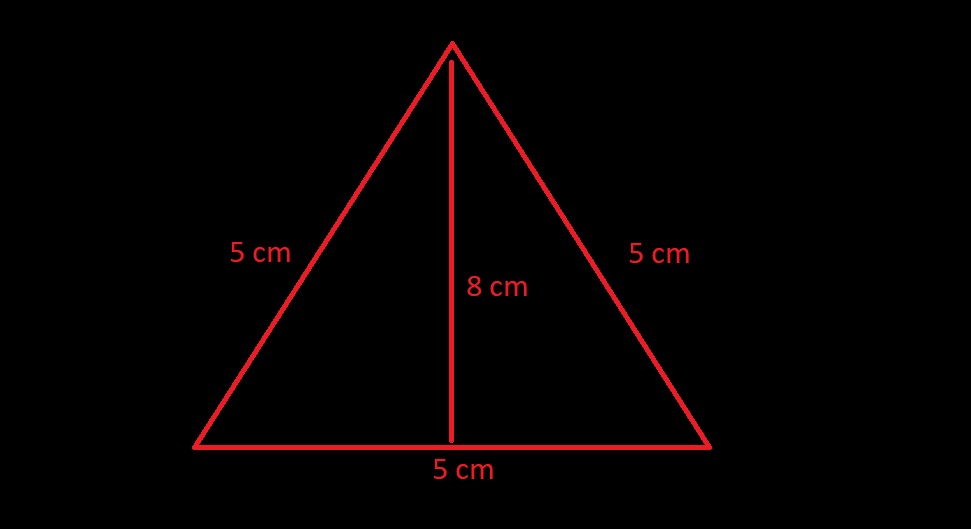
Rumus Luas Segitiga dan Contoh Soal Siku siku Sama Sisi Sumber : sekolah.divedigital.id
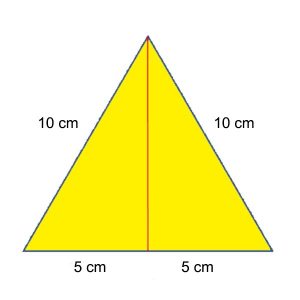
Rumus Luas Segitiga Materi Lengkap Contoh Soal Sumber : nilaimutlak.id
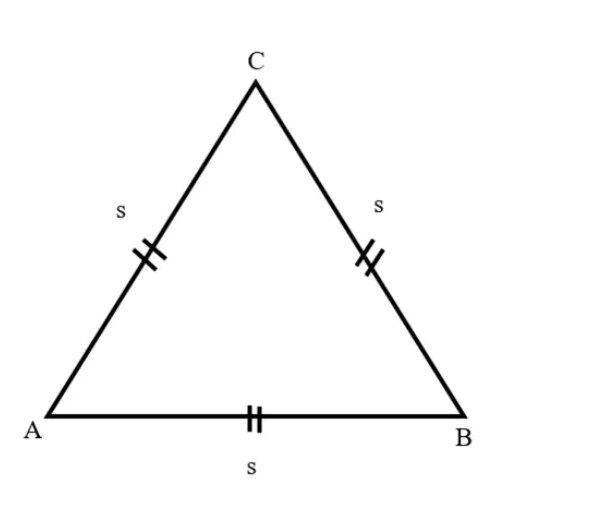
Rumus Luas Dan Keliling Segitiga Lengkap Dengan Contoh Soal Sumber : caraharian.com

Pembahasan Rumus Luas Segitiga Dan Contoh Soalnya Sumber : rumusmatematika.id
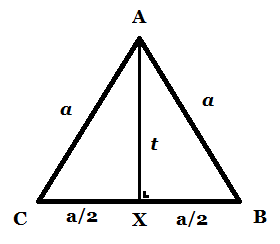
Cara Cepat Menghitung Luas Segitiga Sama Sisi Sumber : mafia.mafiaol.com

Cara Cepat Menghitung Keliling Garis Tinggi dan Luas Sumber : ukurandansatuan.com
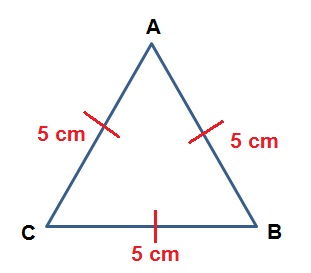
Rumus Luas dan Keliling Segitiga Sama Sisi Lengkap Dengan Sumber : pospelajaran.blogspot.com

Segitiga Sumber : www.slideshare.net
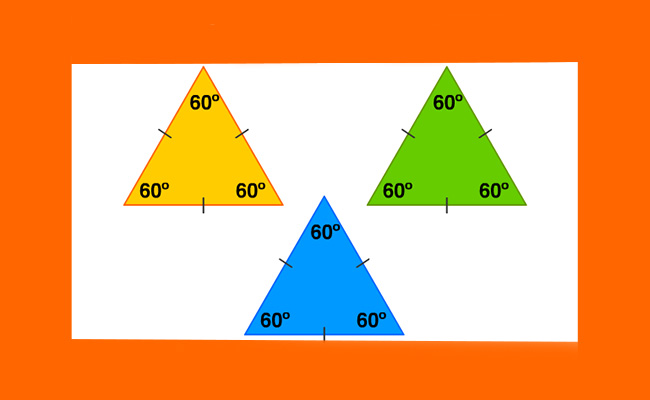
Rumus Segitiga Sama Sisi Luas Tinggi Keliling Sumber : www.perpusku.com

uds Keliling segitiga sama sisi 600x300p Ukuran Dan Satuan Sumber : ukurandansatuan.com
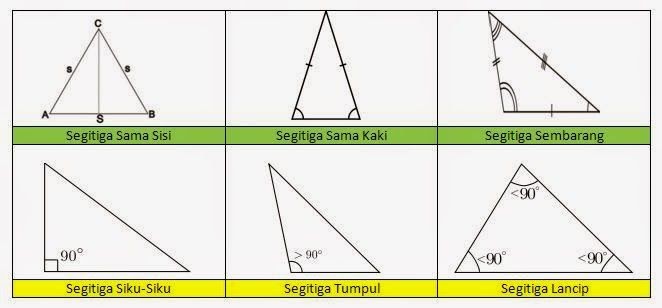
Contoh Soal Luas Dan Keliling Segitiga Sama Sisi Kunci Ujian Sumber : kunciujianbaru.blogspot.com
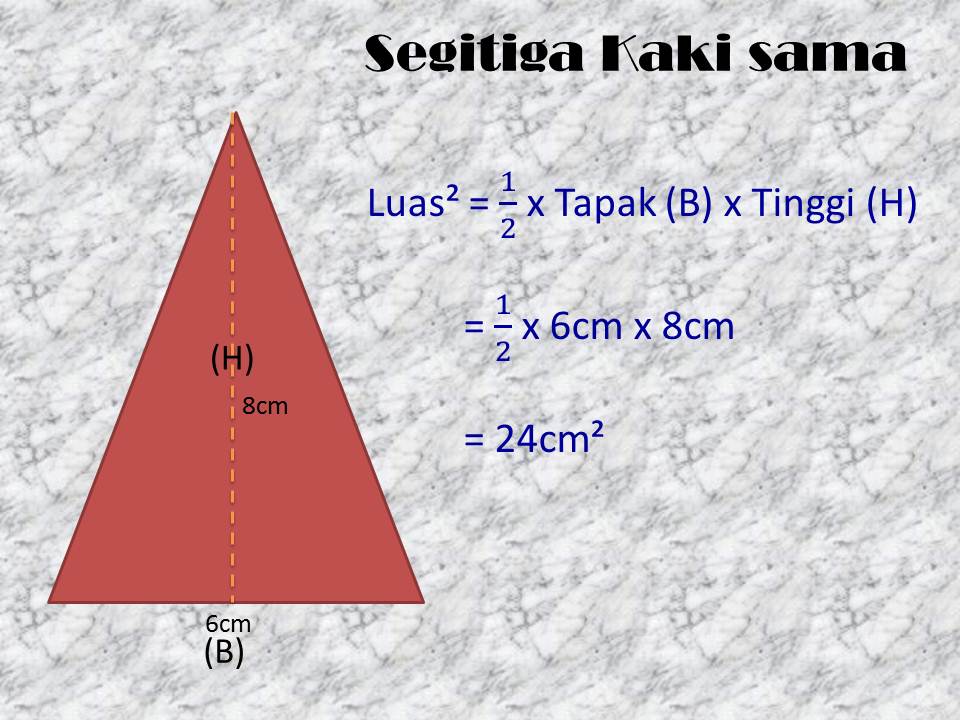
Formula pengiraan luas BENTUK DAN RUANG Sumber : amazingmaths2011.blogspot.co.id
hitunglah luas segitiga sama sisi jika diketahui panjang sisinya 8 cm, tentukan luas segitiga sama sisi dengan panjang sisinya adalah 4 ˆš 3 cm, contoh soal luas segitiga sama sisi, rumus segitiga siku siku, luas segitiga sama sisi dengan panjang 4 akar 2 cm adalah, tentukan luas segitiga sama sisi yang panjang sisinya 9 ˆš3, luas segitiga sama sisi yang panjang sisinya 6 cm adalah, luas segitiga sama sisi yang memiliki panjang sisi 8 cm adalah,
Luas Segitiga Sama Sisi

Rumus luas segitiga dan keliling segitiga Fisika dan Sumber : fismath.com
LUAS PERMUKAAN LIMAS segitiga sama sisi

Cara Menghitung Luas Segitiga dan Keliling Segitiga Sumber : www.andik.my.id
Luas Segitiga Sama Sisi Mudah Tanpa perlu
17 02 2022 Rumus lebar segitiga sama sisi Kita telah mengetahui seandainya rumus umum dari segitiga yaitu L a x t Namun pada segitiga sama sisi untuk menghitung luasnya selain memakai rumus diatas juga sanggup memakai rumus cepat untuk mencari luasnya yaitu L a 4 x 3 a merupakan panjang sisi segitiga Rumus Tinggi Segitiga Sama Sisi

Rumus Luas dan Keliling Segitiga Sama Sisi Trimatematika Sumber : trimatematika.wordpress.com
Luas Segitiga Sama Sisi Rumus Lengkap 10
06 01 2022 Mengenal Rumus Luas Segitiga Sama Sisi Segitiga ialah sebuah poligon dengan tiga titik sudut dan juga tiga sudut Menjadikannya sebagai salah satu bentuk dasar dalam geometri Segitiga sama sisi mempunyai sifat tersendiri yaitu Ketiga sisi nya sama panjang Memiliki tiga buah sudut yang sama besar Mempunyai tiga sumbu simetri Kalau diperhatikan atap kediaman mempunyai unsur segitiga di

Rumus Luas Segitiga dan Contoh Soal Siku siku Sama Sisi Sumber : sekolah.divedigital.id
Pelajari Rumus Luas Segitiga Sama Sisi dan
20 01 2022 tutorial video cara menghitung lebar permukaan Limas segitiga sama sisi About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy Safety How YouTube

Rumus Luas Segitiga Materi Lengkap Contoh Soal Sumber : nilaimutlak.id
Rumus Luas Segitiga dan Contoh Soal Siku siku

Rumus Luas Dan Keliling Segitiga Lengkap Dengan Contoh Soal Sumber : caraharian.com
Luas dan keliling segitiga sama sisi YouTube
Pembahasan Rumus Luas Segitiga Dan Contoh Soalnya Sumber : rumusmatematika.id
Segitiga Sama Sisi Rumus Gambar Sifat dan
Praktek mengajar

Cara Cepat Menghitung Luas Segitiga Sama Sisi Sumber : mafia.mafiaol.com
LUAS SEGITIGA SAMA SISI MATEMATIKA SMP
17 07 2022 Jadi besar dari segitiga siku siku diatas ialah 42 CM persegi 4 Soal Luas Segitiga Sama Sisi Sebuah bangunan segitiga sama sisi seperti diatas masing masing sisinya merupakan 5 CM sedangkan untuk tingginya merupakan 8 CM pertanyaanya berapakah leluasa dari segitiga tersebut Diketahui A 5 CM T 8 CM Dijawab Rumus a x t 2 5cm x 8cm 2 40 cm 2
Cara Cepat Menghitung Keliling Garis Tinggi dan Luas Sumber : ukurandansatuan.com

Rumus Luas dan Keliling Segitiga Sama Sisi Lengkap Dengan Sumber : pospelajaran.blogspot.com
Segitiga Sumber : www.slideshare.net

Rumus Segitiga Sama Sisi Luas Tinggi Keliling Sumber : www.perpusku.com

uds Keliling segitiga sama sisi 600x300p Ukuran Dan Satuan Sumber : ukurandansatuan.com

Contoh Soal Luas Dan Keliling Segitiga Sama Sisi Kunci Ujian Sumber : kunciujianbaru.blogspot.com

Formula pengiraan luas BENTUK DAN RUANG Sumber : amazingmaths2011.blogspot.co.id

